
Um histograma é um gráfico com barras, verticais ou horizontais, utilizado para representar uma distribuição de frequências; tendo, no eixo X, dados organizados em classes (faixas, grupos, ou intervalos), em que a altura da coluna é proporcional à frequência da variável na sua classe (no caso em que os intervalos são iguais). Veja, a seguir, dicas para construir um histograma visualmente bom:
- Tanto quanto possível, utilize sempre intervalos iguais, pois, nesse caso, a altura de cada coluna será igual à frequência da variável, e isso facilita a comparação entre os intervalos;
- Procure fazer os intervalos de modo que proporcionem o melhor agrupamento possível;
- Utilize um número razoável de intervalos, lembre-se de que o objetivo é que o gráfico seja visualmente amigável, facilitando o entendimento do comportamento da variável.
Origem do Histograma
Segundo várias fontes, inclusive Lexico.com (iniciativa conjunta da Universidade de Oxford e Dictionary.com), a origem da palavra “histograma” teria vindo do grego “istos” (mastro, rede) e “gramma” (escrito, carta), ou seja, a palavra significaria escrito (ou desenhado) em colunas. O termo teria sido cunhado pelo matemático inglês, Karl Pearson, em 1895, considerado o criador o histograma.
Diferença entre Histograma e Gráfico de Barras
Enquanto um gráfico de barras relaciona uma variável no eixo X, com uma variável, no eixo Y; um histograma relaciona um intervalo de uma variável no eixo X, com sua frequência, no eixo Y. Enquanto que o gráfico de barras mostra a relação entre duas variáveis, o histograma mostra o comportamento da variável. Veja os exemplos, a seguir:
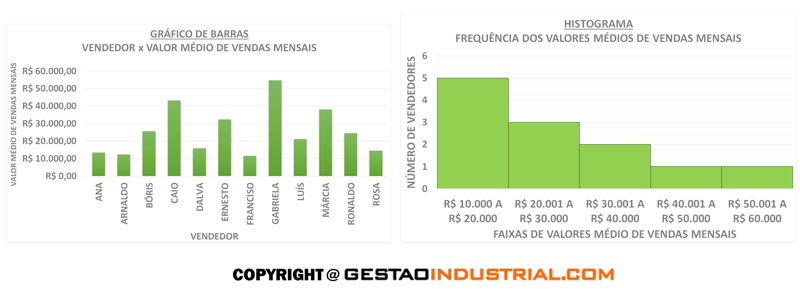
No gráfico de barras vemos a relação de cada vendedor com o valor médio de vendas mensais, e dá pra ver que a Ana está vendendo pouco mais de 10 mil por mês; mas, no histograma, vemos a frequência que determinado valor médio de vendas mensais ocorre, e dá pra ver que há 5 vendedores vendendo um valor médio de 10 mil a 20 mil no mês.
Os Precursores
Um dos precursores no uso do gráfico de barras é o economista escocês, William Playfair, que o utilizou para representar os valores de exportação e importação do ano de 1780, entre a Escócia e diversos outros países.
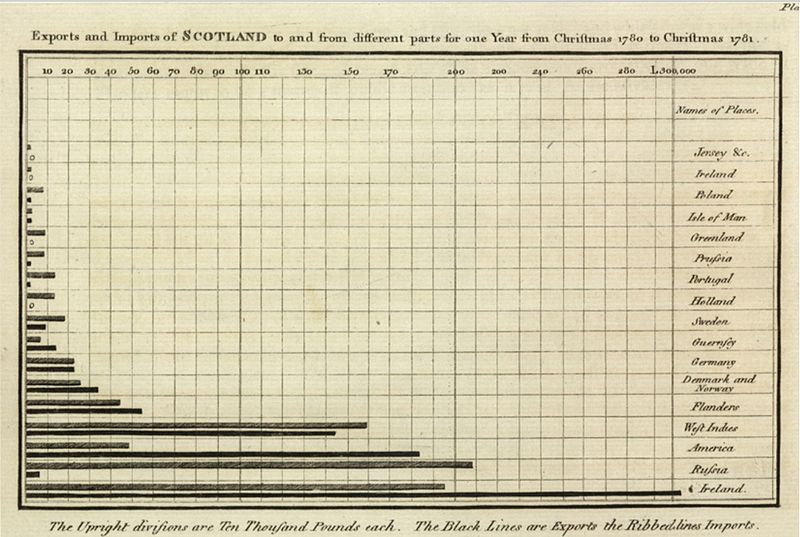
O matemático inglês, Karl Pearson, como já dissemos, é considerado o precursor no uso do histograma, em 1895, e é a ele quem se atribui, também, ter cunhado o nome “histograma”.
Exemplos de Uso do Histograma
Vamos ver um exemplo com dados coletados de testes feitos com um motor ao final de uma linha de montagem. O teste é feito em 100% dos produtos, e a planilha de dados mostra o momento em que cada falha ocorre. Veja, a seguir, uma amostra da planilha de dados dos testes:
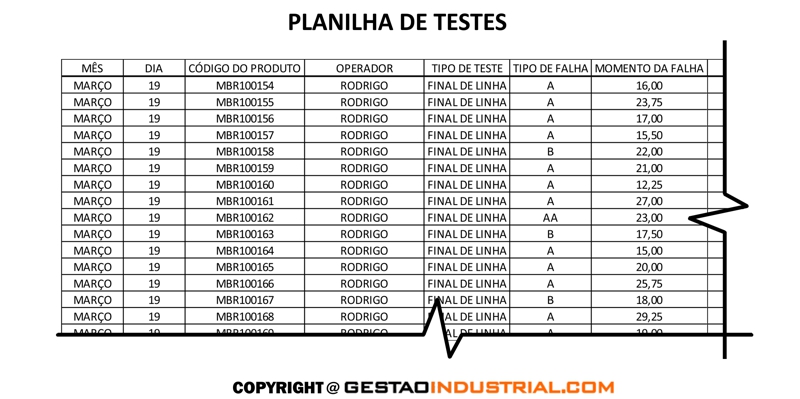
As planilhas com dados reportados ao longo de um mês foram tabuladas, resultando na tabela a seguir:
| MOMENTO DA FALHA (MINUTOS) | QUANTIDADE DE FALHAS |
| ATÉ 5 MINUTOS | 40 |
| DE 5,1 A 10 | 60 |
| DE 10,1 A 15 | 70 |
| DE 15,1 A 20 | 95 |
| DE 20,1 A 25 | 80 |
| DE 25,1 A 30 | 55 |
| MAIS DE 30 | 50 |
O histograma resultante é o seguinte:
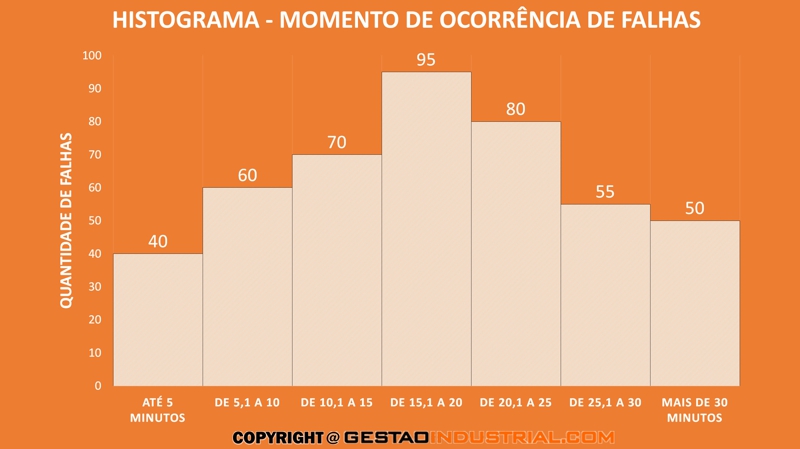
Com base nisso, vê-se, claramente, que as falhas estão ocorrendo mais frequentemente no intervalo de 15,1 a 20 minutos, sendo esse o momento mais crítico do teste. Em conjunto, as áreas de Qualidade, Engenharia, e Produção podem trabalhar para investigar e buscar as causas desse problema.
Outro Exemplo: Ao final de um ano, o gerente financeiro da empresa queria ver o perfil dos clientes, baseado no valor médio mensal comprado (valor total de compras do ano dividido por 12). Trata-se de uma empresa que vende autopeças para grandes distribuidores e redes. Veja, a seguir, uma amostra da planilha de faturamento:
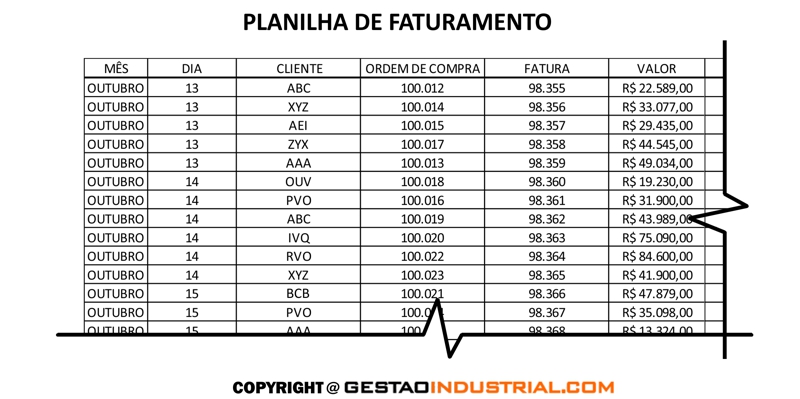
O dados tabulados pelo gerente estão na tabela, a seguir:
| VALOR MÉDIO DE FATURAMENTO MENSAL | QUANTIDADE DE CLIENTES |
| ATÉ R$10.000,00 | 5 |
| DE R$10.001,00 A R$20,000,00 | 7 |
| DE R$30.001,00 A R$40.000,00 | 13 |
| DE R$40.001,00 A R$50.000,00 | 22 |
| DE 50.001,00 A R$60.000,00 | 15 |
| DE R$60.001,00 A R$70.000,00 | 6 |
| DE 70.001,00 A R$80.000,00 | 7 |
| DE R$80.001,00 A R$90.000,00 | 4 |
| DE R$90.001,00 A R$100.000,00 | 3 |
| MAIS DE R$100.000,00 | 2 |
O histograma resultante é o seguinte:
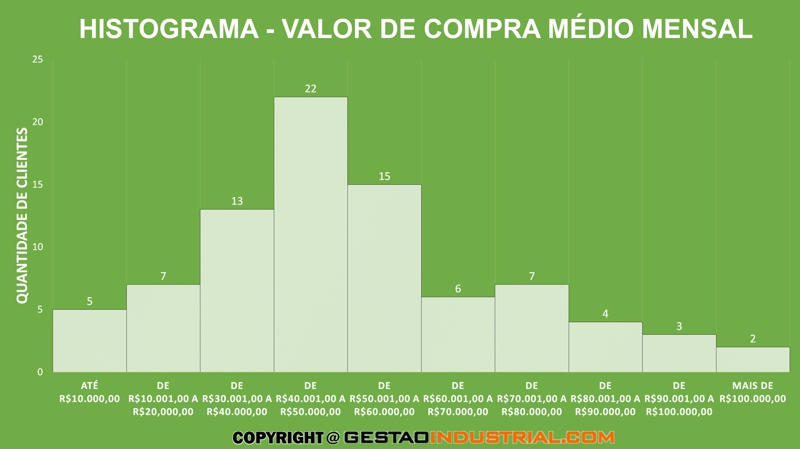
Com base nesse histograma, pode-se traçar estratégias para aumentar o faturamento dos 25 clientes (5 + 7 + 13) que têm feito compras com faturamento médio mais baixo.
Veja a planilha com esse histograma e os outros deste post, na página de downloads.
Histograma com Intervalos Diferentes
Tudo que vimos até agora, foi relativo a histogramas com intervalos iguais. Mas, e quando não são iguais? Se, no caso de intervalos iguais, a altura da coluna é igual à frequência da variável naquele intervalo, quando os intervalos não são iguais, a altura da coluna será igual à densidade de frequência.
A densidade de frequência é igual à frequência dividida pelo intervalo:
densidade de frequência = frequência / intervalo
Vamos voltar ao exemplo do histograma das médias de frequência dos valores médios de vendas mensais e mudar o intervalo. A seguir, veja o nosso gráfico, com os dados originais:
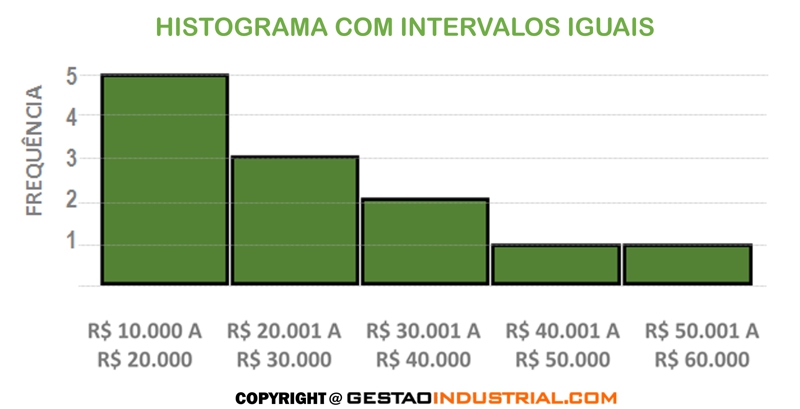
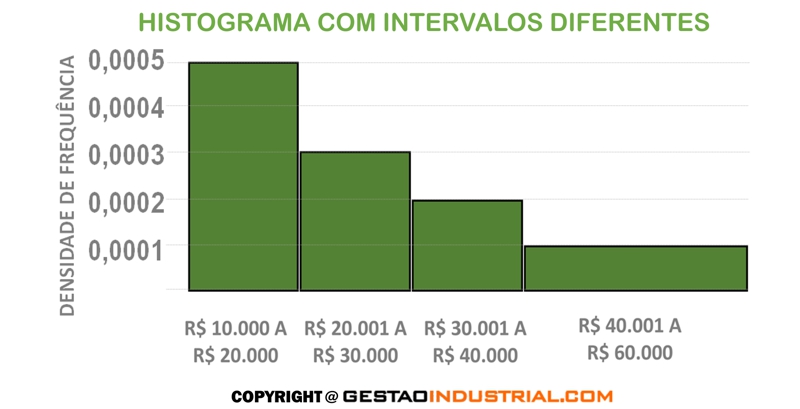
Agora, queremos mudar o último intervalo para R$40.001 a R$60.000. Devemos, então, calcular a densidade de frequência, conforme a tabela:
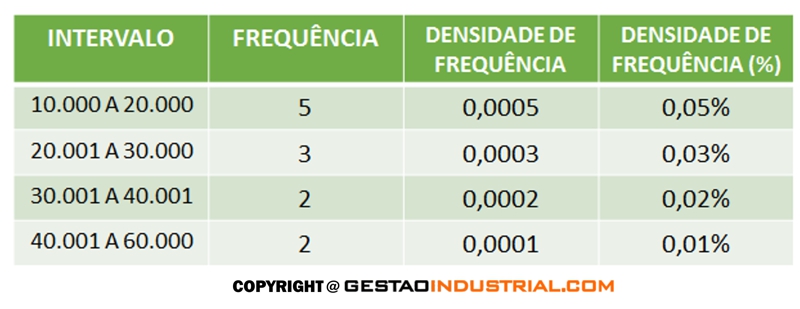
Veja que transformamos a densidade de frequência em percentual, apenas para tornar a informação mais amigável. Com esses dados, o novo histograma deve ser o seguinte:
Existem várias ferramentas básicas da Qualidade, mas, sem dúvida, o histograma é uma ferramenta simples e visualmente esclarecedora, e, em conjunto com outras, pode ajudar em várias situações dentro de uma Organização.
