Decidindo com conhecimento e informação!
Métodos de Análise de Alternativas Econômicas
Ao nos depararmos com várias alternativas econômicas, seja para aprovar a compra de um equipamento, ou o início de um novo projeto, temos a necessidade de poder compará-las com o objetivo de poder selecionar a mais adequada ao negócio.

O método mais comum é o do Valor Presente, em que trazemos todos os valores envolvidos para a data atual e assim comparamos a melhor alternativa. Mas também temos outros métodos, dentre os quais os mais importantes são: Valor Futuro, Valor Anual, Custo/Benefício, Taxa de Retorno e Prazo de Retorno.
O Método do Valor Futuro é aquele em que levamos todos os valores envolvidos para uma determinada data futura.
O Método do Valor Anual é aquele em que transformamos todos os valores em parcelas com uma determinada periodicidade, que pode ser anual ou não.
O Método da Relação Custo/Benefício é aquele em que, em cada alternativa, definimos a razão entre os valores dos custos envolvidos e os valores dos benefícios envolvidos. Devemos esperar, obviamente, relações abaixo de 1, indicando benefícios maiores que os custos.
O Método da Taxa de Retorno é aquele em que calculamos a taxa de juros envolvida, essa taxa representará a taxa de retorno do projeto, também chamada, nesse caso, de mínima atratividade do projeto. Desse modo poderemos compará-la com as taxas de outros projetos e, inclusive, com a taxa de mercado, podendo assim definir a melhor alternativa.
No caso do Método do Prazo de Retorno, todas as alternativas devem apresentar o prazo de retorno do investimento, sendo que é desejável o menor prazo de retorno do investimento.
Para relembrar alguns conceitos da Matemática Financeira, fundamentais para as análise das alternativas econômicas, expomos abaixo um conteúdo básico e objetivo sobre o tema que, esperamos, possa ajudar.
Conceitos Básicos de Matemática Financeira
Período de Capitalização: é o período em que determinada quantia rende um valor, aplicada a uma taxa de juros i. O número de períodos de capitalização é representado por n.
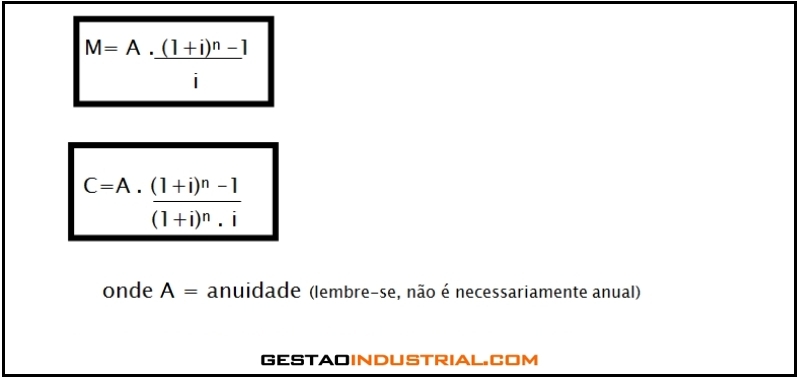
Montante M: é a quantia existente ou equivalente no instante final n. Pode ser encontrado em alguns livros com outros nomes, como: valor futuro, valor de resgate ou valor capitalizado.
Capital C: é a quantia existente ou equivalente no instante inicial. Pode ser chamado de valor presente, valor atual ou valor de aplicação.
Taxa de Juros i: índice de rendimento por período de capitalização é a razão entre os juros recebidos e o capital inicialmente aplicado.
Juros J: é a remuneração do capital emprestado ou aplicado.
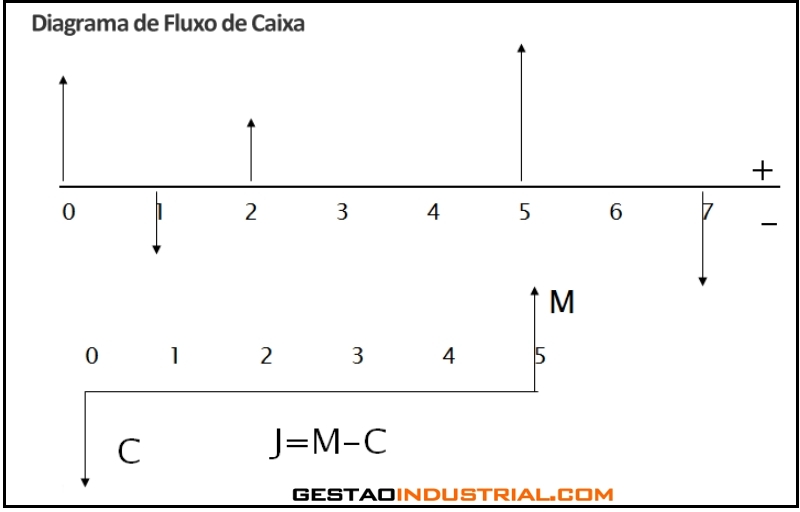
Fluxo de Caixa: é uma sucessão de recebimentos ou pagamentos, num determinado período de tempo.
Recebimento: é representado por uma fecha para cima, no diagrama de fluxo de caixa, é positivo.
Pagamento: é representado por uma fecha para baixo, no diagrama de fluxo de caixa, é negativo.
Diagrama de Fluxo de Caixa: é a representação gráfica do fluxo de caixa.
Juros Simples
Capitalização Simples: é aquela em que a taxa de juros incide somente sobre o capital inicial; não incidindo pois, sobre os juros acumulados.
Fórmulas:

Juros Compostos
Capitalização Composta: é aquela em que a taxa de juros incide, não somente sobre o capital inicial, mas também sobre os juros já calculados até então.
Fórmulas:

Taxa Interna de Retorno
Também chamada (por incrível que pareça) de taxa externa de retorno ou de taxa verdadeira de retorno. É aquela taxa capaz de tornar equivalentes os capitais futuros e o capital na data zero. Ou, dizendo de outra forma: é a taxa que equaliza o valor presente de um ou mais recebimentos com o valor presente de um ou mais pagamentos.
Taxa Mínima de Atratividade
Ao desejar investir uma quantia, comparamos, geralmente, os prováveis dividendos que serão proporcionados por este investimento (com a taxa mínima de atratividade) com os de outros investimentos disponíveis. A taxa de juros que o dinheiro investido irá proporcionar, via de regra, deverá ser superior a uma taxa pré-fixada, com a qual, fazemos a comparação.
Tal taxa de juros comparativa e pré-fixada, que é oferecida pelo mercado, é chamada de taxa mínima de atratividade, taxa de equivalência ou taxa equivalente de lucros.
Taxa Proporcional e Taxa Equivalente
O conceito de taxas proporcionais é utilizado somente para capitalização simples, no sentido de que o valor dos juros é linearmente proporcional ao tempo. Assim, a taxa de 3% ao mês é proporcional a 18% ao semestre ou 36% ao ano. A taxa de 12% ao ano é proporcional a 1% ao mês.
Taxas equivalentes, conceito utilizado na capitalização composta, são aquelas que produzem o mesmo montante ao final de um determinado período, pela aplicação de um mesmo capital inicial.

Correção Monetária
Correção Monetária: É o reajuste de valores de acordo com determinados índices que traduzem uma variação de preços, de modo a anular ou, pelo menos, minimizar os efeitos da perda do poder aquisitivo.
Taxa Real e Taxa Aparente: Sendo
- r= taxa real
- f= taxa de inflação ou taxa de correção monetária
- i= taxa aparente
teremos a fórmula abaixo:

Inflação Acumulada: Para o cálculo da inflação acumulada de determinado período, utilizamos a seguinte fórmula:
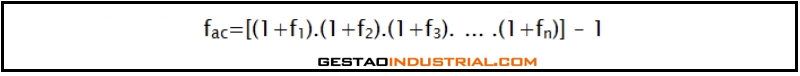
Onde
- fac= inflação acumulada num determinado período
- f1, f2, f3, … , fn = taxas de inflação de cada mês do período em questão
Equivalência de Capitais
Sejam P1, P2, … , Pn os valores nominais de n capitais resgatáveis nos prazos t1, t2, … , tn, respectivamente. Dizemos que os capitais acima considerados são equivalentes em determinada época E, se apresentarem valores iguais quando avaliados nesta mesma época segundo uma mesma taxa de juros i.

Que é a condição para os capitais serem equivalentes.
Séries Financeiras (Anuidades)
Anuidades: São uma sucessão de pagamentos ou de recebimentos A1, A2, … , An e com vencimentos sucessivos n1, n2,…,nn.
Atenção, este termo-anuidade-não se refere apenas a períodos anuais, necessariamente; mas é um termo já consagrado pelos grandes autores para representar alguma periodicidade, que pode ser mensal, semanal, etc..
Classificação: As anuidades podem ser:
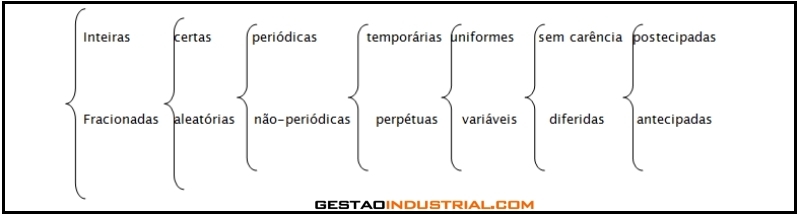
O caso mais comum, tanto em problemas, quanto na prática comercial, e é o que estudamos nesta apostila, é a anuidade inteira, certa, periódica, temporária, uniforme, imediata e postecipada (ou seja, colocada no final do mês).
Fórmulas:
Empréstimos (Planos de Amortização)
Planos de Amortização :
São formas pré-estabelecidas de pagamentos de empréstimos, onde sempre utilizamos o conceito de juros compostos. São três tipos principais: sistema francês de amortização, sistema de amortização constante e sistema misto.
Sistema de Amortização Francês (Tabela Price):
Consiste em um plano de amortização de uma dívida em prestações periódicas, iguais e sucessivas, dentro do conceito de termos vencidos, em que o valor de cada prestação ou pagamento é composto por duas parcelas distintas: juros e capital (amortização).
Sistema de Amortização Constante (SAC):
Neste sistema, apenas as amortizações são constantes. Os juros são maiores no início, pois o capital é maior.
Sistema de Amortização Misto (SAM):
É um plano de pagamento cujas prestações são resultantes da média aritmética dos valores das prestações dos planos SAC e PRICE, correspondentes aos respectivos prazos. Os valores das parcelas de amortização e juros resultam da mesma regra.
